How to Implement a Heap in JavaScript and Perform Push, Pop, and Heapify Operations

What is a Heap?

A heap is a specialized tree-based data structure that satisfies the heap property. In a heap, for any given node (except the root), the node's value is always ordered with respect to its parent. 

This ordering can be one of two types:

1. Max-Heap: In a max-heap, for every node except the root, the value of a node is, at most, the value of its parent. This means the largest element is at the root, and elements get smaller as you traverse down the tree. In simpler terms, all the child nodes must be smaller than their parent.

2. Min-Heap: In a min-heap, for every node except the root, the value of a node is at least the value of its parent. This means the smallest element is at the root, and elements get larger as you traverse down the tree.

Characteristics of a Heap

A heap is also a complete binary tree, which means all levels of the tree are fully filled, and if the last level is not complete, the nodes are filled from left to right.

Priority queues are often implemented using a binary heap, although it’s not the only way to implement one. It is used when we want to order a queue based on some priority value.

This means that each element has a certain priority. The priority of the elements determines the order in which elements are removed from the priority queue.

Implementation of Heaps

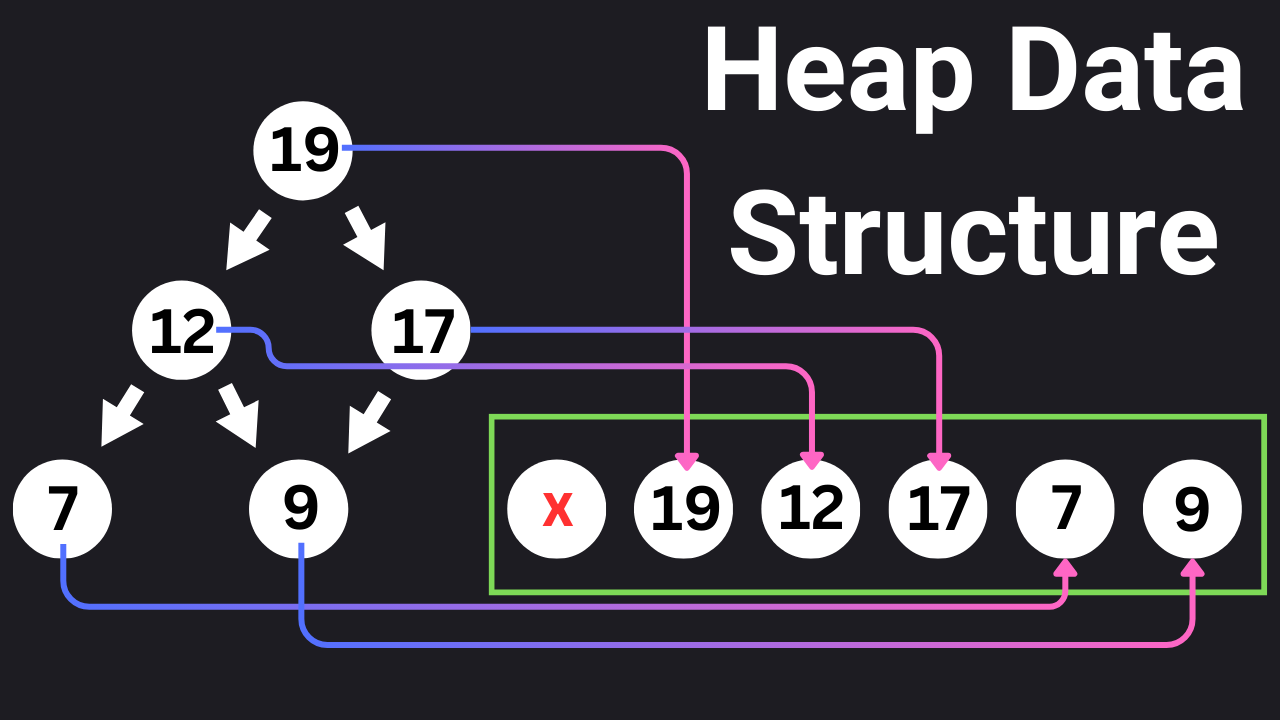
The easiest way to implement a heap is by not using a binary tree but rather an array data structure. This is because they are complete binary trees. 

With arrays, we also ensure that there are no gaps in the tree (except for the last level, which must be filled from left to right), allowing for a compact representation without any wasted space.

If you look closer at this binary heap, you’ll notice that each node has an index below it, representing its index in the array representation.

If we transition to the array view, this is how our binary heap looks like:

We use 1-based indexing, meaning we don’t count the 0th item in the array, and the root starts from index 1. In this case, if a node is at index i in the array:

• Its left child, if it exists, is at index 2i.

• Its right child, if it exists, is at index 2i+1.

• Its parent, if it exists and i is not 1 (the root), is at index ⌊i/2⌋.

This means that the root starts at arr[1], the left node is arr[2], the right node is arr[3], and so on.

This representation takes advantage of the properties of a complete binary tree and allows for easy navigation between parent and child nodes without needing pointer/reference-based tree node structures.

Operations

The primary operations on Heaps are inserting an element, extracting the maximum/minimum element, and heapifying to maintain the heap property.

I recommend you check out the visual representations of these operations to understand them better.

Insertion

class Heap {
    constructor() {
        // Initialize heap with null at index 0 for 1-based indexing
        this.heap = [null];
    }

    // Inserts a new value into the heap
    insert(value) {
        this.heap.push(value);
        this.heapifyUp(this.heap.length - 1);
    }

    // Heapify up for maintaining the heap property after insertion
    heapifyUp(index) {
        while (index > 1 && this.heap[Math.floor(index / 2)] < this.heap[index]) {
            this.swap(Math.floor(index / 2), index);
            index = Math.floor(index / 2);
        }
    }

    // Swaps two values in the heap
    swap(index1, index2) {
        [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
    }
}

The insert method of this Heap class adds a new value to the heap and then ensures the heap maintains its properties by rearranging elements if necessary. Here's how it works:

1. It adds the new value to the end of the array (this.heap). This step keeps the tree complete, meaning all levels of the tree are fully filled except possibly for the last level, which is filled from left to right.

2. Then, it calls theheapifyUp method with the index of the newly added value to maintain the heap property. 

How heapifyUp Works:

1. While the current node has a parent and violates the heap property (i.e., it’s larger than its parent for a max heap), swap it with its parent.

2. Continue this process until the heap property is restored (either the current node is no longer larger than its parent or it becomes the root).

The worst-case time complexity of the insert method is O(log n), as the newly added element might need to be compared and possibly swapped at each level from the bottom of the tree to the top to maintain the heap property.

Extraction

Extraction is when we remove the root element from the Heap. If we just want to look at the top item of the heap (minimum or maximum item), we can access it under the first index this.heap[1] with O(1) time complexity.

class Heap {
    constructor() {
        this.heap = [null];
    }

    // Removes and returns the maximum value from the heap
    extractMax() {
        if (this.heap.length < 2) return null; // Heap is empty

        const maxValue = this.heap[1];
        this.heap[1] = this.heap.pop(); // Move the last value to the root
        this.heapifyDown(1);

        return maxValue;
    }

    // Heapify down for maintaining the heap property after extraction
    heapifyDown(index) {
        let largest = index;
        const left = 2 * index;
        const right = 2 * index + 1;

        if (left < this.heap.length && this.heap[left] > this.heap[largest]) {
            largest = left;
        }

        if (right < this.heap.length && this.heap[right] > this.heap[largest]) {
            largest = right;
        }

        if (largest !== index) {
            this.swap(index, largest);
            this.heapifyDown(largest);
        }
    }

    // Swaps two values in the heap
    swap(index1, index2) {
        [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
    }
}

The extractMax method removes and returns the maximum value from a max heap. Here's how it works, step by step, followed by its time complexity:

1. Checks if the heap is empty: If the heap contains fewer than two elements (considering the first element is null for 1-based indexing), it means the heap is empty, and the method returns null.

2. Removes the maximum value: The maximum value in a max heap is always at the root, which is this.heap[1]. This value is stored in maxValue to be returned later.

3. Rearranges the heap: Moves the last element in the heap to the root position (this.heap[1]). This action maintains the completeness of the binary tree but might violate the heap property. To restore the heap property, heapifyDown is called starting from the root.

4. Returns maxValue: Finally, the method returns the value that was originally at the root of the heap, which is the maximum value of the heap.

How heapifyDown Works

1. heapifyDown maintains the heap property by comparing the current node with its left and right children to find the largest value among them.

2. If the current node is not the largest, it’s swapped with the largest of its children. This might violate the heap property in the subtree where the swap happened, so heapifyDown is called recursively for the index of the child that was swapped.

3. It continues until the heap property is restored for the entire heap, meaning the current node is larger than its children or it has no children.

The worst-case time complexity of extractMax is O(log n) because it might need to perform a comparison and swap at each tree level to restore the heap property after removing the maximum element.

Heapify 

The heapify operation is used to convert an arbitrary array into a heap. This is done by applying heapifyDown from the last non-leaf node down to the root.

class Heap {
    constructor() {
        this.heap = [null];
    }
    
    // Builds a heap from an unsorted array
    buildHeap(arr) {
        this.heap = [null, ...arr]; // Reset heap and set values
        const startIdx = Math.floor(this.heap.length / 2);
        for (let i = startIdx; i >= 1; i--) {
            this.heapifyDown(i);
        }
    }

    heapifyDown(index) {
        // same as before
    }
}

How buildHeap Works

1. The method starts by setting the heap property to a new array that starts with null (for 1-based indexing) followed by the elements of the input array arr.

2. It calculates the starting index for the heapification process as the last non-leaf node’s index, which is Math.floor(this.heap.length / 2). This is because all nodes beyond this point are leaf nodes that already satisfy the heap property.

3. It iterates backwards from the starting index to the root of the heap (index 1), calling heapifyDown for each node. This process ensures that the heap property is established for each node, effectively converting the unsorted array into a heap.

The time complexity of building a heap from an unsorted array is O(n), where n is the number of elements in the array. This might seem counter-intuitive at first because heapifyDown has a time complexity of O(log n), and it's being called in a loop.

However, not all calls to heapifyDown go the full height of the tree. Calls for nodes closer to the bottom of the tree have a shorter path to traverse, and the number of nodes at each level doubles as you move up the tree, balancing out the cost. When averaged over all elements, this results in a linear time complexity for building the heap.